Algoritmalarda Big-O Gösterimi – Big-O Notation

Bir önceki makalemde algoritmalarda karmaşıklık analizinin ne olduğunu ve en iyi ve en kötü senaryoların hangi durumlarda ortaya çıktığından bahsetmiştim. Bu makalede ise algoritmaların Big-O (Büyük-O) analizini nasıl yapacağınızı anlatacağım.

Big-O gösterimi, tasarladığımız bir algoritmanın performansını ve zaman karmaşıklığını(time complexity) ölçmek için kullandığımız en önemli araçlardan biridir. Başka bir deyişle, algoritmanın etkinliğini tanımlamak için kullandığımız dil ve metriktir.

Big-O kavramının ne olduğunu bilmeden algoritma tasarlamak geliştirdiğiniz algoritmaya zararlar verebilir.

Algoritmaları tasarlarken farklı veri yapılarına ihtiyaç duyarız. Array, LinkedList, Queue, Stack, Binary Tree, Graph gibi. Ya da aynı veri yapısı üzerinde (örneğin Array) farklı algoritmalar çalıştırabiliriz. Bubble Sort, Insertion Sort, Quick Sort, Heap Sort, Merge Sort sıralama algortimaları buna örnektir.

Seçtiğimiz veri yapıları algoritmanın kalitesine, tükettiği kaynaklara, hızına ve kullanışına farklı etkiler yapar. Bu yüzden yazılım geliştiricilerin bu konuyu iyi bir şekilde anlaması lazım.

Bazı Big-O Terimleri ve Senaryoları

En yaygın çalışma zamanları O(log n), O(nlog n), O(n), O(n²)’ dir. Ancak çalışma zamanlarının kesin bir listesi yoktur. Çünkü çalışma zamanı hesaplanırken birçok değişken göz önüne alınır.

Sık karşılaştığımız Big-O zamanları şunlardır:

• O(1) → Constant
• O(N) → Linear
• O(N²) → Quadratic
• O(logN) → Logarithmic
• O(NlogN) → Linearithmic
• O(2^N)→ Exponential
• O(N!) → Factorial

Burada N, veri setinin büyüklüğü ya da eleman sayısı iken c, sabit bir değerdir.

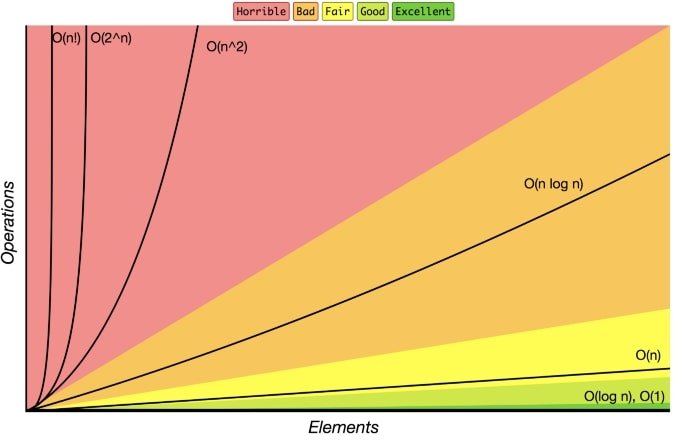
Yukarıdaki grafikte veri setine ve yapılan işleme göre algoritmanın Big-O sınıflandırması yer almaktadır.

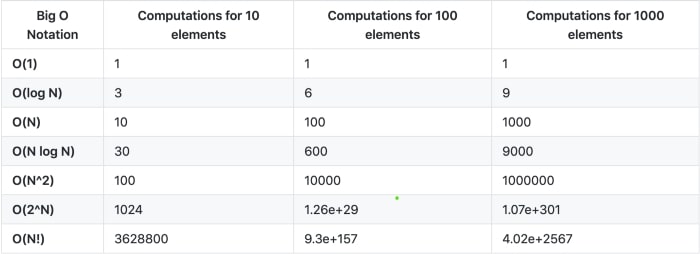
Bu tabloda ise en çok kullanılan Big-O terimlerinin farklı büyüklüklerdeki veri girdilerine göre karşılaştırmaları yer almaktadır.

Şimdi bazı Big-O büyüklüklerini örneklerle daha iyi anlayalım.

1) Sabit Karmaşıklık (Constant Complexity) – O(1)

Sabit karmaşıklıkta algoritmaya girilen veri seti ne kadar büyük olursa olsun çalışma zamanı ve kullanılan kaynak miktarı sabittir.

• O(1) zamanda çalışır.

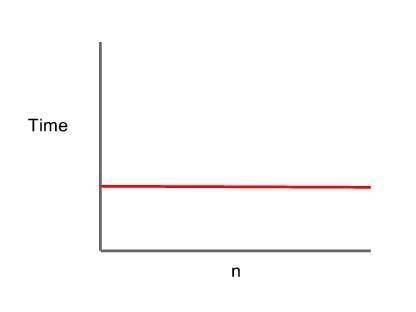
Örneğin,

var arr = [ 1,2,3,4,5];

arr[1]; // => 2

Algoritmaya girdi olarak girilen dizinin boyutu ne olursa olsun çalışma zamanı hep sabit kalacaktır. Çünkü biz dizinin 1. elemanını buluyoruz.

2) Doğrusal Karmaşıklık (Linear Complexity) – O(N)

Doğrusal karmaşıklıkta algoritmaya girdiğimiz veri setinin büyüklüğü arttıkça çalışma zamanı da doğrusal olarak artar. Yani girilen veri setinin büyüklüğü ile çalışma zamanı arasında doğru orantı vardır.

• O(N) zamanda çalışır.

Örnek olarak elimizde bulunan bir CD yığını düşünelim. Biz bu CD yığınının en altındaki CD ye ulaşmak için CD sayısı kadar zaman harcamalıyız. Eğer CD sayısı artarsa harcadığımız zamanda orantılı olarak artacaktır.

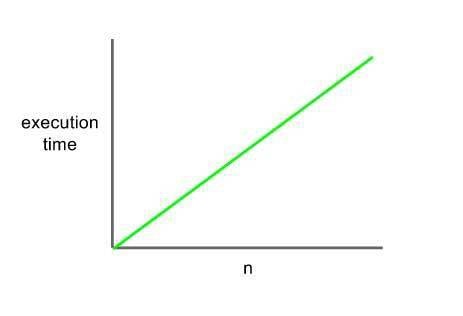
for(int i=0; i<n; i++){
    print("Hello World");
}

Burada program çıktı olarak n tane “Hello World” yazacak. Dolayısıyla n sayısı arttıkça programın çalışma zamanı da doğrusal olarak artacaktır.

3) Quadratic Complexity – O(N²)

Basitçe, çalışma zamanı girdi büyüklüğünün karesiyle doğru orantılıdır. Yani eğer girdi büyüklüğü 2 ise 4 işlem, 8 ise 16 işlem gerçekleşir.

• O(N²) zamanda çalışır.

Genellikle sıralama(sorting) algoritmalarında bu karmaşıklık görülür.

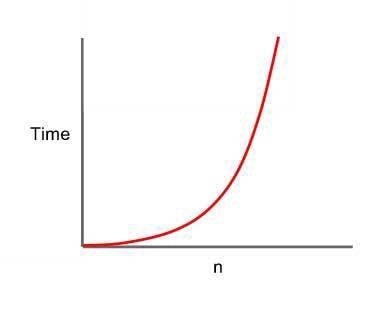
İç içe iki tane for döngüsü buna çok iyi bir örnektir.

for(int i=0; i<arr.length; i++){
    for(int j=0; j<arr.length; j++){
        print("Hello World");
    }
}

Tek bir for döngüsünde çalışma zamanı O(N) olur. Ancak iç içe 2 tane for döngüsü kullanıldığı zaman çalışma zamanı O(N²)’dir.

4) Logaritmik Karmaşıklık (Logarithmic Complexity) – O(log N)

Logaritmik karmaşıklık genel olarak her seferinde problemi ikiye bölen algoritmalarda karşımıza çıkar. Diğer bir deyişle, algoritmayı çalıştırmak için geçen süre N girdi boyutunun logaritması ile orantılıysa bu algoritma logaritmik zaman karmaşıklığına sahiptir.

• O(logN) zamanda çalışır.

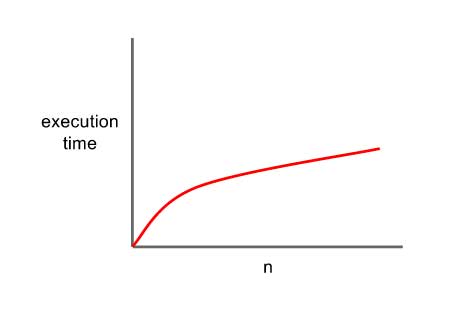
for(let i=n; i>1; i/=2){
    console.log(i);
}

5) Linearitmik Complexity – O(NlogN)

Linearitmik zaman karmaşıklığı, doğrusal bir algoritmadan biraz daha yavaştır, ancak yine de ikinci dereceden bir algoritmadan çok daha iyidir.

• O(NlogN) zamanda çalışır.

6) Üstel Karmaşıklık (Exponential Complexity) – O(2^N)

Üstel karmaşıklık (2 tabanında) logaritmanın tersi şekilde işlem sayısı üstel olarak algoritmalarda görülür.

İşlem açısından katlanarak artan bu tip fonksiyonlar sisteminizi tüketir. Bu tip hesaplamalardan olabildiğince kaçınmak gerekir.

• O(2^N) zamanda çalışır.

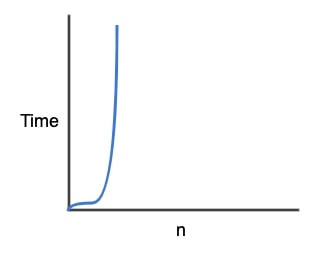
Üstel karmaşıklığa örnek olarak bir dizinin tüm alt kümelerini verebiliriz.

powerset('') // ...
// n = 0, f(n) = 1;
powerset('a') // , a...
// n = 1, f(n) = 2;
powerset('ab') // , a, b, ab...
// n = 2, f(n) = 4;
powerset('abc') // , a, b, ab, c, ac, bc, abc...
// n = 3, f(n) = 8;
powerset('abcd') // , a, b, ab, c, ac, bc, abc, d, ad, bd, abd, cd, acd, bcd...
// n = 4, f(n) = 16;
powerset('abcde') // , a, b, ab, c, ac, bc, abc, d, ad, bd, abd, cd, acd, bcd...
// n = 5, f(n) = 32;

Burada hiç elemanı olmayan bir dizinin 1 tane alt kümesi varken; diziye bir eleman eklendiğinde 2 tane alt kümesi olur. Ardından diziye bir tane daha eleman eklediğimiz zaman dizinin 4 tane alt kümesi olur. Bu şekilde diziye ne kadar eleman eklersek dizinin alt küme sayısı 2^N oranında artar.

7) Faktöriyel Karmaşıklığı (Factorial Complexity) – O(N!)

Faktöriyel, kendisinden küçük tüm pozitif tam sayıların çarpımıdır. Dolayısıyla faktöriyel karmaşıklığa sahip algoritmaların karmaşıklığı oldukça hızlı büyür. Bu yüzden bu karmaşıklığa sahip algoritmalardan uzak durun.

• O(N!) zamanda çalışır.

getPermutations('ab') // ab, ba...
// n = 2, f(n) = 2;
getPermutations('abc') // abc, acb, bac, bca, cab, cba...
// n = 3, f(n) = 6;
getPermutations('abcd') // abcd, abdc, acbd, acdb, adbc, adcb, bacd...
// n = 4, f(n) = 24;
getPermutations('abcde') // abcde, abced, abdce, abdec, abecd, abedc, acbde...
// n = 5, f(n) = 120;

Son Düşünceler

Bu makalemde algoritmalarda Big-O gösteriminin ne olduğunu ve en çok karşılaştığımız Big-O terimlerini örnekle anlatmaya çalıştım.

Kaynaklar:

• https://www.bigocheatsheet.com/
• https://falconcoder.com/2019/11/22/algorithm-analysis-with-bigo-notation/
• https://medium.com/kodcular/nedir-bu-big-o-notation-b8b9f1416d30
• https://medium.com/algorithms-data-structures/algoritma-karma%C5%9F%C4%B1kl%C4%B1%C4%9F%C4%B1-big-o-5f14316890a4
• https://medium.com/@busrauzun/cracking-the-coding-interviewdan-notlar-b%C3%B6l%C3%BCm-4-big-o-b9f9ce7fcf13