Algoritamaların Karmaşıklık Analizi – Complexity Analysis

Önceki makalelerimden birinde algoritmalara kısa bir giriş yapmıştım. Bu makalede ise algoritmaların karmaşıklık analizi nedir sorusuna birlikte yanıt arayacağız.

Algoritmaların karmaşıklık analizi, bir algoritmanın çalışması için gereken kaynak miktarının belirlenmesidir. Yani algoritmanın performansını ve kaynak kullanımını ölçen teorik bir çalışmadır.

Gündelik hayatta herhangi bir problemi çözerken birbirinden farklı yollara başvuruz. Aynı şekilde bilgisayar biliminde de belli bir probleme birden fazla çözüm yolu üretmek mümkündür. Tabi ki burada en uygun çözümü, yani algoritmayı seçmek önemlidir. İşte bu yüzden algoritmaların karmaşıklık analizini iyi bilmek gerekiyor. Bir problemi çözmeye çalışırken olası tüm algoritmaları incelemeli ve en uygun olanı seçmemiz gerekiyor.

Algoritma analizi belirli bir programlama dilinden bağımsız şekilde yapılır. Bunun amacı sadece algoritmanın kendisini analiz edip doğru sonuçlara ulaşmaktır.

Bir problemi farklı algoritmalarla çözebiliriz. Ancak problemi çözerken gelişigüzel bir mantık kurmak ya da analiz yapmadan bir algoritma seçmek programdan ödün vermek demektir. Yani algoritma seçerken o probleme en uygun sonucu getirecek olan algoritmayı seçmeliyiz.

Eninde sonunda algoritma bir şekilde tasarlanır ve problem çözülür. Ama her bakımdan en iyi sonucu veren tek bir algoritma vardır.

İşte algoritma analizinin amacı da o en uygun sonucu veren algoritmayı bulmaktır. Kısaca algoritmaları birbirleriyle karşılaştırmak ve performansını ölçmek.

Algoritmanın Performans Kriterleri Nelerdir?

Yukarıda da belirttiğim gibi bir problemi farklı algoritmalar tasarlayarak çözmek mümkün. Ancak bu çözümlerin birbirlerine karşı mutlaka avantajları ve dezavantajları olacaktır.

Örneğin, hızlı çalışan bir algoritma bellekten fazla alan tüketirken, tam tersi daha az bellek tüketen bir algoritma da daha yavaş çalışır.

Bir algoritmanın analizini yaparken bazı soruları göz önünde bulundurmalıyız:

• Problemi çözmek için ne kadar bellek tüketecek?
• Problemin çözülmesi ne kadar zaman alacak?
• Daha fazla veri girildiğinde algoritma nasıl davranıyor? Yavaşlıyor mu yoksa hızlanıyor mu?

Algoritma performansında iki temel kriter vardır: zaman(time) ve alan(space). Algoritmalar bu iki kriterden en uygun sonucu alacak şekilde tasarlanmalıdır.

• Zaman (time)
  • Algoritma ne kadar hızlı çalışıyor?
  • Algoritmanın çalışması için gereken zamanın nasıl tahmin edilir? Gereken zaman nasıl azaltılabilir?
  • Algoritmanın çalışma zamanını etkileyen faktörler nelerdir?

• Alan (space)
  • Algoritmada hangi veri yapıları kullanılmalıdır?
  • Kullanılan veri yapıları ne kadar yer kaplar?
  • Daha iyi sonuç veren bir veri yapısı kullanılabilir mi?

Algoritma analizinde temel olarak yürütme zamanı ve zaman karmaşıklığı üzerinde durulur. Ancak tüm bu soruların cevabını verebilmek için alan karmaşıklığı, alan maliyeti, zaman karmaşıklığı ve yürütme zamanı gibi kavramları da incelemek gerekiyor.

Alan Maliyeti (Space Coast)

Basitçe, algoritmanın çalışması için gereken bellek miktarına denir. Alan maliyeti programın kodları, yığın ve bellek için gerekli olan tüm alanlardır. S(n) ile gösterilir.

Örneğin, 2 bytelık tamsayı olan n elemanlı bir küme için alan maliyeti bağıntısı S(n) = 2n şeklinde gösterilir.

Yürütme Zamanı veya Çalışma Zamanı (Running Time)

Çalışma zamanı algortimadaki döngüler, atama, karşılaştırma ve aritmetik operasyonlar gibi işlemlerin kaç kere yürütüldüğünü veren bağıntıdır. Diğer bir ifadeyle, N boyutlu bir algoritmayı çalıştırmak için gereken zamana denir. T(N) ile gösterilir.

• NOT: Çalışma zamanı, zaman karmaşıklığıyla benzerdir. Algoritmadaki eleman sayısı arttığında çalışma zamanı, zaman karmaşıklığı olarak adlandırılır. Ancak yine de çalışma zamanı ve zaman karmaşıklığını birbirinden ayıran bazı noktalar vardır.

Çalışma zamanının hesaplanırken dikkat edilmesi gereken birimler şunlardır:

• Döngü sayıları (for döngüsü, while döngüsü vb.)
• Atama sayıları
• İşlem sayıları
• Deyimler (seçim deyimleri, yineleme deyimleri vb.)
• Dosya erişim sayısı

Zaman Karmaşıklığı (Time Complexity)

Zaman karmaşıklığı, algoritmanın yürütme zamanının derecesinin asimptotik notasyonlarla gösterilmesidir. Bir başka deyişle bir algoritmanın çalışması için gereken süredir. Bu süre ne kadar kısa olursa algoritmanın performansı o kadar iyi olur. Zaman karmaşıklığını bir algoritmanın performansı olarak düşünebiliriz.

Bu süre milisaniyeleri hesaplayarak değil, yapılan işlem sayısına göre hesaplanmaktadır. Tabi ki bu hesaplama yapılırken algoritmadaki veri setinin büyüklüğüne ve sırasına dikkat edilir.

Amaç, giriş boyutu ve zaman arasındaki karmaşıklığı azaltmaktır. Yani detayları es geçerek çalışma süresini indirgemektir.

İşte bu yüzden algoritma sonsuza giderken asimptotik gösterimde sabitler ve katsayılar gibi büyümeye fazla etkisi olmayan kısımlar hesaplanmaz. Böylece geriye algoritmanın büyümesinde asıl etkiye sahip olan değerler kalır ve gerçek fonksiyona göre yaklaşık bir değer hesaplanır.

Bir bilgisayarın donanım özellikleri ne kadar iyi olursa olsun, her zaman en iyi performans gösteren algoritmayı seçmek gerekir. Böylece donanımda yapılan iyileştirmelerle algoritma daha da iyi performans göstermiş olur.

Alan Karmaşıklığı (Space Complexity)

Alan karmaşıklığı, bir algoritmanın bir girdi boyutu için çıktı üretirken ihtiyaç duyduğu bellek miktarıdır. Yani buna alan maliyetini ölçmek demektir diyebiliriz.

Daha iyi alan karmaşıklığına sahip olan algoritma bellekten daha az alan tüketir. Algoritmanın performansını artırmak için sistem belleğini artırmak ilk akla gelen çözüm olsa da, her zaman daha az alan tüketen bir algoritma tasarlamak daha mantıklıdır.

Alan karmaşıklığı, algoritmayı çalıştıran sistem, derleyici ve programlama dili gibi çeşitli faktörlere bağlıdır. Bu yüzden algoritmanın kendisini analiz ederken bu faktörleri dikkate almamalıyız.

Ne yazık ki, algoritma performansında zaman ve alan verimliliği birbirine terstir. Yani hız arttıkça bellek tüketimi artar. Ya da tam tersi.

Örnek olarak merge sort, bubble sort ve in-place heap algoritmalarını inceleyelim. Merge sort en hızlı ancak en fazla bellek tüketen algoritmadır. Bubble sort ise tam tersine en yavaş ancak en az bellek tüketen algoritmadır. In-place heap ise bu iki algoritmanın arasında performans gösteren daha dengeli bir algoritmadır.

Notation

Notation, karmaşıklık analizi yapılan bir algoritmanın performansının farklı gösterimler ile temsil edilmesidir. Yukarıda da belirttiğim gibi bir algoritma girilen verilerin büyüklüğüne göre farklı performans gösterebilir.

Örneğin, 1 Kb lık veriden çıktı üreten algoritma hızlı çalışırken, aynı algoritmaya 1 mb veri girildiğinde çıktıyı daha yavaş üretebilir. Bu nedenle, olabilecek tüm durumların karmaşıklığını analiz etmemiz gerekiyor.

Zaman karmaşıklığında genel olarak üç temel asimptotik notasyon vardır. Bunlar:

• Big-O Notasyonu
• Omega Notasyonu
• Teta Notasyonu

Bu notasyonlar arasında biz en çok Big-O notasyonuyla ilgileneceğiz. Bunun nedenini açıklayacağım ancak önce best case, average case ve worst case kavramlarını inceleyelim.

Best Case (En İyi Durum)

Algoritmanın karmaşıklığı hesaplanırken en iyi sonucun elde edildiği duruma denir. Algoritmanın en az adımda ve zamanda çalıştığı durumdur.

Çalışma zamanında bir alt sınırdır. Grafik gösterimlerinde alt sınır (lower bound) olarak görürüz.

Omega notasyonu ( Ω ) da denir.

Average Case (Ortalama Durum)

Adından da anlaşılacağı gibi, best case ile worst case arasında ortaya çıkan durumdur.

Teta notasyonu ( θ ) da denir.

Worst Case (En Kötü Durum)

Algoritmanın en fazla adımda ve zamanda çalıştığı durumdur. Olabilecek tüm olumsuz durumları kapsar.

Big O notasyonu ( O ) da denir.

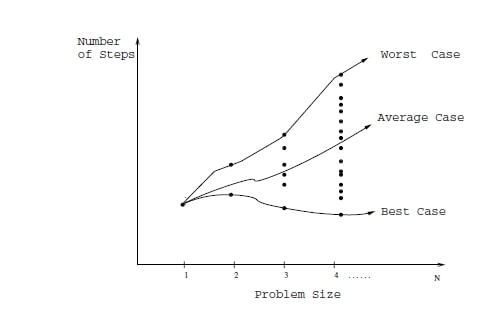
Karmaşıklık analizinde verileri sonsuza giderken değerlendiririz. Worst case de bize algoritmanın sonsuza giderkenki durumunu verir. İşte bu yüzden daha çok Big-O notasyonuyla yani üst sınır (upper bound) değeri ilgileniriz. Bu şekilde algoritmanın en kötü senaryosunu inceleyebiliriz.

Şimdi bu notasyonlara kısaca bir göz atalım.

Omega Notasyonu Big-Ω Notasyonu

Omega notasyonu (Omega Notation), asimptotik alt sınırı(lower bound) ifade eder. Bu notasyonla algoritma zaman açısından en iyi duruma(best case) ulaşmış olur. Büyük-O gösteriminin tersidir.

Teta Notasyonu Big-θ Notasyonu

Teta gösterimi, alt sınır(lower bound) ile üst sınır(upper bound) arasında kalan ortalama bir karmaşıklığı ifade eder.. Yani, Big-O notasyonu ile Big Omega notasyonu arasında yer alır.

Big-O Notasyonu Büyük O Gösterimi

Big O Notasyonu, algoritma analizindeki zaman karmaşıklığında üst sınırı(upper bound) tanımlar. Algoritmanın büyüme hızını (growth rate) temsil etmek için kullanılır.

Bir algotirmanın karmaşıklık analizi yapıldıktan sonra ortaya çıkan ifadeleri sadeleştirerek algoritmanın en sade karmaşıklığının bulmamızı sağlar.

Mesela, 6n³+8n+4 ifadesini sadeleştirerek O(n³) şeklinde gösterebiliriz.

Son Düşünceler

Özet geçecek olursak, bir algoritmanın karmaşıklık analizi yapılırken temel olarak alan karmaşıklığı ve zaman karmaşıklığı incelenir. Burada amaç her zaman en iyi performans gösteren algoritmayı bulmaktır.

Bu makalede algoritmaların karmaşıklık analizinin ne olduğunu, neden önemli olduğunu ve Big-O gösteriminin neden öenmli olduğunu anlatmaya çalıştım. Tabi ki bu konular daha ayrıntılı şekilde incelenebilir.