Complexity Analysis of Algorithms

I gave a brief introduction to algorithms in one of my previous articles. In this article, we will look for an answer to the question of what is the complexity analysis of algorithms.

Complexity analysis of algorithms is the determination of the amount of resources required for an algorithm to work. In other words, it is a theoretical study that measures the performance and resource usage of the algorithm.

While solving any problem in daily life, we resort to different ways. In the same way, it is possible to produce more than one solution to a certain problem in computer science. Of course, it is important to choose the most appropriate solution, namely the algorithm. That is why it is necessary to know the complexity analysis of algorithms well. When trying to solve a problem, we need to examine all possible algorithms and choose the most suitable one.

Algorithm analysis is done independently of a particular programming language. The purpose of this is only to analyze the algorithm itself and reach the correct results.

We can solve a problem with different algorithms. However, while solving the problem, using arbitrary logic or choosing an algorithm without analysis means sacrificing the program. In other words, when choosing an algorithm, we should choose the algorithm that will bring the most appropriate result to that problem.

Ultimately, the algorithm is somehow designed and the problem is solved. But there is only one algorithm that works best in all respects.

The purpose of algorithm analysis is to find the algorithm that gives the most appropriate result. Briefly, comparing algorithms with each other and measuring their performance.

What are the Performance Criteria of the Algorithm?

As I mentioned above, it is possible to solve a problem by designing different algorithms. However, these solutions will definitely have advantages and disadvantages over each other.

For example, a fast-running algorithm will consume more memory, while an algorithm that consumes less memory will run slower.

When analyzing an algorithm, we should consider some questions:

• How much memory will it consume to solve the problem?
• How long will it take to solve the problem?
• How does the algorithm behave when more data is entered? Is it slowing down or speeding up?

There are two basic criteria in algorithm performance: time and space. Algorithms should be designed to get the most appropriate result from these two criteria.

• Time
  • How fast does the algorithm work?
  • How to estimate the time needed for the algorithm to run? Can the time required be reduced?
  • What are the factors affecting the running time of the algorithm?

• Alan
  • What data structures should be used in the algorithm?
  • How much space do the data structures used take up?
  • Can a data structure be used that works better?

In algorithm analysis, the main focus is on execution time and time complexity. However, in order to answer all these questions, it is necessary to examine concepts such as space complexity, space cost, time complexity and running time.

Space Cost

Simply, it is the amount of memory required for the algorithm to run. The space cost is all the space required for the program’s codes, stack and memory. It is denoted by S(n).

For example, for a set with n elements, which are 2 byte integers, the space cost relation is represented as S(n) = 2n.

Running Time

The runtime is the relation that gives the number of times operations such as loops, assignment, comparison, and arithmetic operations in the algorithm are executed. In other words, it is the time required to run an N-dimensional algorithm. It is denoted by T(N).

• NOTE: Runtime is similar to time complexity. When the number of elements in the algorithm increases, the runtime is called time complexity. However, there are still some points that separate runtime and time complexity.

The units to be considered when calculating the working time are:

• Loop counts (for loop, while loop etc.)
• Assignment numbers
• Number of transactions
• Idioms (selection statements, iteration statements, etc.)
• File access count

Time Complexity

Time complexity is the degree of execution time of the algorithm in asymptotic notations. In other words, it is the time required for an algorithm to run. The shorter this period, the better the performance of the algorithm. We can think of time complexity as the performance of an algorithm.

This time is calculated not by calculating milliseconds, but by the number of transactions made. Of course, while making this calculation, attention is paid to the size and order of the data set in the algorithm.

The aim is to reduce the complexity between input size and time. In other words, it is to reduce the working time by skipping the details.

This is why parts that do not have much effect on growth, such as constants and coefficients, are not calculated in asymptotic notation as the algorithm goes to infinity. Thus, the values ​​that have the main effect on the growth of the algorithm remain and an approximate value is calculated according to the real function.

No matter how good a computer’s hardware features are, it is always necessary to choose the best performing algorithm. Thus, with the improvements made in the hardware, the algorithm performs even better.

Space Complexity

Space complexity is the amount of memory an algorithm needs to produce output for an input size. So we can say that it means measuring the cost of space.

The algorithm with better space complexity consumes less memory space. Although increasing the system memory to increase the performance of the algorithm is the first solution that comes to mind, it is always more logical to design an algorithm that consumes less space.

Domain complexity depends on several factors, such as the system running the algorithm, the compiler, and the programming language. That’s why we shouldn’t take these factors into account when analyzing the algorithm itself.

Unfortunately, time and space efficiency are inverse to each other in algorithm performance. That is, the higher the speed, the higher the memory consumption. Or vice versa.

As an example, let’s examine the merge sort, bubble sort and in-place heap algorithms. Merge sort is the fastest but most memory consuming algorithm. Bubble sort, on the other hand, is the slowest but least memory consuming algorithm. In-place heap is a more balanced algorithm that performs between these two algorithms.

Notation

Notation is the representation of the performance of an algorithm for which complexity analysis is performed, with different representations. As I mentioned above, an algorithm may perform differently depending on the size of the data entered.

For example, while an algorithm that produces output from 1 Kb of data works fast, when 1 MB of data is entered into the same algorithm, it can produce output more slowly. Therefore, we need to analyze the complexity of all possible situations.

There are generally three basic asymptotic notations in time complexity. These:

• Big-O Notation
• Omega Notation
• Theta Notation

Among these notations, we will be most interested in the Big-O notation. I will explain why, but first, let’s examine the concepts of best case, average case and worst case.

Best Case

The situation in which the best result is obtained when calculating the complexity of the algorithm is called. It is the case where the algorithm runs in the least number of steps and time.

It is a lower bound at runtime. We see it as lower bound in graphic representations.

Also called omega notation ( Ω ).

Average Case

As the name suggests, it is the case between best case and worst case.

Also called theta notation ( θ ).

Worst Case

It is the case where the algorithm runs in the most steps and time. It covers all possible negative situations.

Also called Big O notation ( O ).

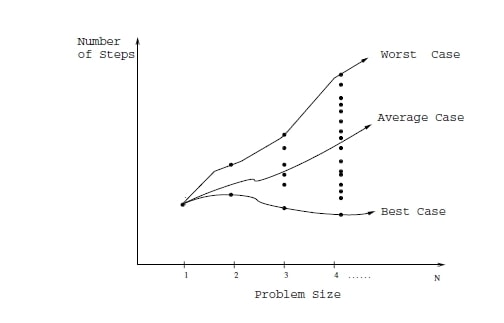
In complexity analysis, we evaluate data going to infinity. The Worst case also gives us the state of the algorithm going to infinity. That’s why we’re more interested in Big-O notation, the upper bound value. In this way, we can examine the worst-case scenario of the algorithm.

Let’s take a quick look at these notations.

Omega Notation (Big-Ω Notation)

Omega notation refers to the asymptotic lower bound. With this notation, the algorithm reaches the best case in terms of time. It is the opposite of Big-O notation.

Theta Notation (Big-θ Notation)

Theta notation denotes an average complexity that lies between the lower bound and the upper bound. That is, it lies between Big-O notation and Big Omega notation.

Big-O Notation (Big-O Notation)

Big-O Notation defines the upper bound in time complexity in algorithm analysis. It is used to represent the growth rate of the algorithm.

It allows us to find the simplest complexity of the algorithm by simplifying the expressions that emerge after the complexity analysis of an algorithm.

For example, we can simplify the expression 6n³+8n+4 to O(n³).

Final Thoughts

To summarize, while performing the complexity analysis of an algorithm, the domain complexity and time complexity are mainly examined. The goal here is always to find the best performing algorithm.

In this article, I tried to explain what complexity analysis of algorithms is, why it is important, and why Big-O representation is important. Of course, these issues can be studied in more detail.